BUNGA

NILAI UANG

Modal adalah uang dan sumber daya yang diinvestasikan.

Bunga (interest) adalah pengembalian atas modal atau sejumlah uang yang diterima investor untuk penggunaan uangnya di luar modal awal (principal)

Tingkat bunga.

Alasan pengembalian modal dalam bentuk interest (bunga) dan profit :

·       Penggunaan uang melibatkan biaya administrasi

·       Setiap investasi melibatkan resiko

·       Penurunan nilai mata uang yang diinvestasikan

·       Investor menunda kepuasan yang bisa dialami segera dengan menginvestasikan uangnya

Kapan kita menemui tingkat bunga?

·       Kartu kredit

·       Buku tabungan

·       Kredit mobil

·       Saham

·       . . . . . . .

Bunga digunakan untuk menghitung Nilai waktu dari uang

*sedolar hari ini nilainya lebih dari sedolar tahun depan*

Bunga Sederhana

Bunga setiap tahunnya dihitung berdasarkan atas investasi awal. Tidak ada bunga yang dihitung atas bunga yang bertambah.

Notasi:

i = Tingkat bunga per periode (misal 1 tahun)

N = Jumlah periode

P = Deposit awal

F = Nilai masa depan setelah N periode

F = P(1+Ni)

Apa masalahnya?

Jika bank tempat anda menabung menawarkan bunga sederhana. . . .

Apa yang akan anda lakukan?

Bunga Majemuk

Bunga setiap tahun dihitung berdasarkan pada saldo tahun tersebut, termasuk bunga yang bertambah.

F = P(1+ i)N

Secara lebih eksplisit,

FN = P0 1+ i (2.4)

(nilai masa depan dalam periode N, nilai sekarang pada waktu 0)

Oleh karena itu, untuk mencari nilai masa depan pada periode N+n, diketahui nilai sekarang pada periode n,

FN+n = Pn 1+ i (2.5)

Contoh 2.1: pinjaman bank

Anda pergi ke bank dan mencari informasi tentang peminjaman $10,000 selama 10 tahun. Petugasnya mengatakan: “tentu bisa, tinggalkan saja jam Rolex dan cincin bermata intan anda di sini sebagaijaminan, dan kami akan mengurus pinjaman untuk anda dengan tingkat bunga 6% per tahun, dibungakan tahunan”. Dia kemudian memencet kalkulatornya dan mengatakan, di akhir masa 10 tahun, anda akan melakukan satu pembayaran sekaligus sebesar F dolar untuk membayar pinjaman anda. Berapakah F?

i = 6% = 0.06

N = 10

F = P(1+I)N = 10,000 * (1+0.06)10 = $17,908

Kebalikan proses:

Mencari Nilai Sekarang, diberikan Nilai Masa Depan

Karena F = P (1+i)N (2.3)

Maka P = F / (1+i)N (2.3a)

Contoh 2.2 : pinjaman bank

Berapa nilai sekarang dari $17,908 sepuluh tahun dari sekarang, jika nilai waktu dari uang adalah 6% dibungakan tahunan?

i = 6% = 0.06

N = 10

P = F / (1+I)N = 17,908 / (1+0.06)10 = $10,000

(heran???)

A.  Cash Flow

Cash flow adalah tata aliran uang masuk dan keluar per periode waktu pada suatu perusahaan. Cash flow terdiri dari:

-         cash-in (uang masuk), umumnya berasal dari penjualan produk atau manfaat terukur (benefit);

-         cash-out (uang keluar), merupakan kumulatif dari biaya-biaya (cost) yang dikeluarkan.

Dalam suatu investasi secara umum, cash flow akan terdiri dari empat komponen utama, yaitu:

1.     Investasi, biaya yang ditanamkan dalam rangka menyiapkan kebutuhan usaha untuk siap beroperasi dengan baik. Biaya ini biasanya dikeluarkan pada awal-awal kegiatan usaha dalam jumlah yang relatif besar dan berdampak jangka panjang untuk kesinambungan usaha tersebut. Investasi sering juga dianggap sebagai modal dasar usaha yang dibelanjakan untuk penyiapan dan pembangunan sarana prasarana dan fasilitas usaha termasuk pengembangan dan peningkatan sumber daya manusia.

2.    Operational cost, biaya yang dikeluarkan dalam rangka menjalankan aktivitas usaha tersebut sesuai dengan tujuan. Biaya ini biasanya dikeluarkan secara rutin atau periodik waktu tertentu dalam jumlah yang relaif sama atau sesuai dengan jadwal kegiatan/produksi.

3.    Maintenance cost, biaya yang diperuntukkan dalam rangka menjaga / menjamin performance kerja fasilitas atau peralatan agar selalu prima dan siap untuk dioperasikan.

4.    Benefit/manfaat, penerimaan dari suatu investasi yang berasal dari pendapatan atas pelayanan fasilitas atau penjualan poduk yang dihasilkan dan manfaat terukur lainnya selama umur penggunaan, ditambah dengan nilai jual investasi saat umurnya habis.

Penyusunan cash flow pada dasarnya dapat dilakukan dengan dua metode, yaitu metode tabel dan metode grafis. Namun, untuk lebih efektifnya komunikasi biasanya kedua metode tersebut dipakai secara simultan atau dikombinasikan satu sama lain.

Jika cash flow tersebut sudah merupakan perkiraan uang yang akan masuk dan keluar akibat suatu investasi selama umurnya, perlu diketahui apakah investasi tersebut akan menguntungkan atau tidak. Artinya, apakah jumlah uang yang bakal masuk lebih besar dari jumlah uang yang akan keluar? Jika ya, artinya investasi akan menguntungkan (layak ekonomis), dan sebaliknya.

Jika besaran uang yang akan masuk dan keluar tidak berada pada waktu yang sama, sesuai dengan konsep ‘time value of money’ (nilai uang akan berubah bersama waktu), maka diperlukan metode perhitungan tersendiri yang disebut ekuivalensi nilai uang.

B.  Konsep Nilai Uang Terhadap Waktu

Pengambilan keputusan pada analisis ekonomi teknik melibatkan dan menentukan apa yang ekonomis dalam jangka panjang, yang dikenal dengan istilah nilai waktu dari uang (time value of money). Rp 1000,- saat ini lebih berharga bila dibandingkan dengan Rp1000,- pada satu atau dua tahun yang akan datang. Hal itu disebabkan adanya bunga.

C.  Bunga

Bunga (interest) adala uang yang dibayakan untuk penggunaan uang yang dipinjam. Bunga dapat juga diartikan sebagai pengembalian yang bisa diperoleh dari investasi modal yang produktif.

·         Tingkat suku bunga (rate of interest) adalah rasio antara total bunga yang dibebankan atau dibayarkan di akhir periode tertentu, dengan uang yang dipinjam pada awal periode tersebut.

·         Bunga Sedehana (simple interest), perhitungan bunga hanya didasarkan atas besarnya pinjaman semula dan bunga periode sebelumnya yang belum dibayar tidak termasuk faktor pengali bunga. Total bunga yang diperoleh dapat dihitung dengan rumus:

I = P.i.n

Dimana:   I = total bunga tunggal

              P = pinjaman awal

              i = tingkat suku bunga

              n = periode pinjaman

Sedangkan total pembayaran pinjaman yang harus dilakukan pada akhir periode pinjaman, sebesar      F = P + I

Contoh: seseorang meminjam uang sebesar Rp1.000,- selama 3 tahun dengan tingkat suku bunga 10% per tahun. Berapa total pembayaran yang harus dilakukan pada akhir tahun ke-3 jika bunga yang digunakan adalah bunga sederhana?

Jawab:

Total bunga selama 3 tahun, adalah

I = 1.000 × 0,10 × 3 = 300

Total pembayaran yang harus dilakukan pada akhir tahun ke-3, adalah

F = 1.000 + 300 = 1.300

·         Bunga Majemuk (Compound Interest)

Apabila bunga yang diperoleh dalam setiap periode yang didasarkan pada pimjaman pokok ditambah dengan setiap beban bunga yang terakumulasi sampai dengan awal periode tersebut.

Contoh: seseorang meminjam uang Rp1.000,- selama 3 tahun dengan suku bunga 10% per tahun. Berapa total pembayaran yang harus dilakukan pada akhir tahun ke-3 jika bunga yang digunakan adalah bunga majemuk?

Jawab:

Bunga pinjaman tahun berjalan akan menambah jumlah pinjaman di awal tahun berikutnya.

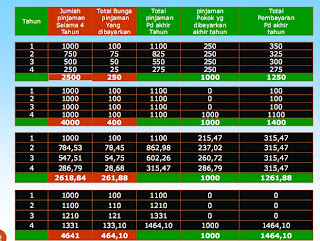
Tabel 1. Contoh Perhitungan Bunga Majemuk

(1) Tahun	(2) Jumlah Pinjaman pada Awal Tahun	(3) = (2) × 10% Bunga Pinjaman Tahun Berjalan	(4) = (2) + (3) Jumlah Pinjaman pada Akhir Tahun
1	1.000,00	100,00	1.100,00
2	1.100,00	110,00	1.210,00
3	1.210,00	121,00	1.331,00

\ Total pembayaran yang harus dilakukan pada akhir tahun ke-3 adalah sebesar Rp1.331,-.

·         Hukum 72

Untuk mengetahui perkiraan waktu yang diperlukan agar nilai investasi tunggal berjumlah dua kali lipat pada suatu tingkat suku bunga majemuk tertentu, digunakan Hukum 72. yaitu : 

72 : n = i  atau

72 : i = n

dimana n = adalah waktu berinvestasi dalam tahun dan i = tingkat pengembalian atau bunga dalam periode n

Contoh :

1. Bapak Ali ingin investasinya menjadi 2 kali lipat dalam waktu 6 tahun. Tingkat investasi atau pengembalian berapa besar yang harus ia dapatkan ? Berarti di sini n=6 , i = ?. Rumus nya 72 : n = i, sehingga 72 : 6 = 12%. Berarti Bapak Ali harus mencari instrumen investasi yang hasilnya 12% agar investasinya dapat menjadi 2 kali lipat dalam waktu 6 tahun.

Aturan 72

Sejumlah uang yang dikenakan bunga majemuk dengan tingkat i% per

periode akan menjadi dua kali lipat jumlahnya dalam periode waktu

sekitar 72/i.

i = 3% ® aturan 72: waktu menjadi 2xlipat adalah 24 periode

(72/3)

® perhitungan: (1.03)N = 2, jadi N = 1.03log 2 = 23.4

® dalam 24 periode: (1.03)24 = 2.03

Ekonomi Teknik

12

i = 9% ® aturan 72: waktu menjadi 2xlipat adalah 8

periode(72/9)

® perhitungan: (1.09)N = 2, jadi N = 1.09log 2 = 8.04

® dalam 8 periode: (1.03)8 = 1.99

i = 12% ® aturan 72: waktu menjadi 2xlipat adalah 6 periode

(72/12)

® perhitungan: (1.12)N = 2, jadi N = 1.12log 2 = 6.12

® dalam 24 periode: (1.03)24 = 1.97

Catatan: 1.03log 2 = ln 2/ln 1.03

http://elib.unikom.ac.id/download.php?id=110118

EKIVALENSI CASHFLOW

Konsep Ekuivalensi

Metode ekuivalen adalah metode mencari kesamaan atau kesetaraan nilai uang untuk waktu yang berbeda.


Dalam perhitungan ekuivalen dibutuhkan data  tentang:

• ƒ suku bunga (rate of interest); 
• ƒ jumlah uang yang terlibat; 
• ƒ waktu penerimaan dan/atau pengeluaran uang; 
• ƒ sifat pembayaran bunga terhadap modal yang  ditanamkan.

Bunga Bunga majemuk majemuk dalam dalam ekuivalensi ekuivalensi

• Single payment/cashflow formulas
• Uniform series formulas
• Linear (Arithmatic) gradient series
• Geometric gradient series

Contoh Soal 

1. Berapakah nilai ekuivalensi masa depan pada akhir tahunke-4 untuk $1000,- diawal tahun pertama pada   tingkat suku bunga 10% per tahun?.

2. Seseorang ingin memiliki $1464,10 dalam 4 tahun.  Berapa besar uang yang harus didepositokan unruk mendapatkan jumlah tersebut pada tingkat suku bunga 10% per tahun?.

3. Seseorang meminjam $1200,- diawal tahun pertama dengan rencana mengembalikannya pada akhir tahun ke-5. Tetapi diawl tahun ke-3 orang tersebut menambah pinjaman sebesar $800,- yang akan dikembalikan

bersamaan dengan pengembalian pinjaman pertama.  Berapa besar uang yang harus dikembalikan di akhir tahun ke-5 jika pinjaman dilakukan dengan tingkat suku bunga

12% per tahun?.

4. Seseorang meminjamkan sejumlah uang diawal tahun pertama dengan rencana akan dikembalikan di akhir

tahun ke-2 sebesar $800,- dan $1200,- di akhir tahun ke-5. Berapa besar uang yang dipinjamkan jika

pinjaman dilakukan pada tingkat suku bunga 15% per  tahun?

5. Si A menginvestasikan sejumlah uang di awal tahun pertama. Di awal tahun ke-3, orang tersebut menambah investasinya sebesar 1,5 kali investasi pertama. Jika tingkat suku bunga 10% per tahun, dan

dikehendak iagar nilai investasinya menjadi $2000,- di akhir tahun ke-5. Berapa besar investasi yang 

dilakukan di awal tahun pertama dan di awal tahun ke-3.?

PRESENT WORTH ANALYSIS

Present worth analysis (Analisis nilai sekarang) didasarkan pada konsep ekuivalensi di mana semua arus kas masuk dan arus kas keluar diperhitungkan dalam titik waktu sekarang pada suatu tingkat pengembalian minimum yang diinginkan (minimum attractive rate of return-MARR). Untuk mencari NPV dari sembarang arus kas, maka kita harus melibatkan faktor bunga yang disebut Uniform Payment Series  - Capital Recovery Factor (A/P,i,n).

Usia pakai berbagi alternative yang akan dibandingkan dan periode analisis yang akan digunakan bisa berada dalam situasi:

1.      Usia pakai sama dengan periode analisis

2.      Usia pakai berbeda dengan periode analisis

3.      Periode analisis tak terhingga

Analisis dilakukan dengan terlebih dahulu menghitung Net Present Worth (NPV) dari masing – masing alternative. NPV diperoleh menggunakan persamaan:

NPV = PW_pendapatan – PW_pengeluaran

Untuk alternatif tunggal, jika diperoleh nilai NPV ≥ 0, maka alternatif tersebut layak diterima. Sementara untuk situasi dimana terdapat lebih dari satu alternatif, maka alternatif dengan nilai NPV terbesar merupakan alternatif yang paling menarik untuk dipilih. Pada situasi dimana alternatif yang ada bersifatindependent, dipilih semua alternatif yang memiliki nilai NPV ≥ 0.

–  Analisis present worth terhadap alternatif tunggal

Contoh:

Sebuah perusahaan sedang mempertimbangkan untuk membeli peralatan seharga Rp 30.000.000,. Dengan peralatan baru itu akan diperoleh penghematan sebesar Rp 1.000.000,- per tahun selama 8 tahun. Pada akhir tahun ke-8, peralatan itu memiliki nilai jual Rp 40.000.000,-.Apabila tingkat suku bunga 12% per tahun, dengan present worth analysis, apakah pembelian tanah tersebut menguntungkan?

Penyelesaian:

NPV = 40.000.000(P/F,12%,8) - 1.000.000(P/A,12%,8) - 30.000.000

NPV = 40.000.000(0.40388) - 1.000.000(4.96764) - 30.000.000

NPV = - 8.877.160

Ø  Oleh karena NPV yang diperoleh < 0, maka pembelian peralatan tersebut tidak menguntungkan.

–           Analisis present worth terhadap beberapa alternatif

§   Usia pakai semua alternatif sama dengan periode analisis

Contoh:

Sebuah perusahaan akan membeli sebuah mesin untuk meningkatkan pendapatan tahunannya. Dua alternatif peralatan masak dengan usia pakai masing-masing 8 tahun ditawarkan kepada perusahaan:

Mesin	Harga beli (Rp.)	Keuntungan per tahun (Rp.)	Nilai sisa di akhir usia pakai (Rp.)
X	2.500.000	750.000	1.000.000
Y	3.500.000	900.000	1.500.000

Dengan tingkat suku bunga 15% per tahun, tentukan mesin mana yang seharusnya dibeli.

Penyelesaian:

Mesin X :

NPV_X = 750.000(P/A,15%,8) + 1.000.000(P/F,15%,8) – 2.500.000

NPV_X = 750.000(4.48732) + 1.000.000(0,32690) – 2.500.000

NPV_X = 1.192.390

Mesin Y :

NPV_Y = 900.000(P/A,15%,8) + 1.500.000(P/F,15%,8) – 3.500.000

NPV_Y = 900.000(4.48732) + 1.500.000(0.32690) – 3.500.000

NPV_Y = 1.028.938

Maka, pilih mesin X

§   Usia pakai alternatif berbeda dengan periode analisis

Pada situasi di mana usia pakai berbeda dengan periode analisis, digunakan asumsi perulangan (repeatability assumption) dengan periode analisis yang merupakan kelipatan persekutuan terkecil dari usia pakai alternative. Dengan asumsi itu, alternative yang telah habis usia pakainya sebelum periiode analisis berakhir akan digantikan oleh alternative yang sama. Arus kas masuk dan arus kas keluar pada periode usia pakai pertama akan berulang pada periode perulangan berikutnya, kecuali jika disebutkan lain. Asumsi ini diterapkan untuk mempermudah pembuatan model dalam pengambilan keputusan.

Contoh:

Sebuah perusahaan akan membeli sebuah mesin untuk meningkatkan pendapatan tahunannya. Dua alternatif mesin ditawarkan kepada perusahaan:

Mesin	Usia pakai (tahun)	Harga beli (Rp.)	Keuntungan per tahun (Rp.)	Nilai sisa pada akhir usia manfaat (Rp.)
X	8	2.500.000	750.000	1.000.000
Y	16	3.500.000	900.000	1.500.000

Dengan tingkat suku bunga 15% per tahun, tentukan mesin yang seharusnya dibeli.

Penyelesaian:

Mesin X:

NPV_X = 750.000(P/A,15%,16) + 1.000.000(P/F,15%,8) + 1.000.000(P/F,15%,16) – 2.500.000(P/F,15%,8)

NPV_X = 750.000(5.95423) + 1.000.000(0.32690) + 1.000.000(0.10686) – 2.500.000(0.32690)

NPV_X     = 1582182,5

Mesin Y:

NPV_Y = 900.000 (P/A,15%,16) + 1.500.000(P/F,15%,16) – 3.500.000

NPV_Y = 900.000 (5.95423) + 1.500.000(0.10686) – 3.500.000

NPV_Y = 2.019.097

Ø  NPV mesin Y, Rp 2.019.097,- lebih besar daripada NPV mesin X, Rp 1.582.182,50,- Maka dipilih mesin Y.

–             Periode Analisis Tak Terhingga

Pada situsi ini di mana periode analisis tidak terhingga, perhitungan NPV dari semua arus masuk dan arus keluar dilakukan dengan metode capitalized worth(nilai modal). Jika hanya unsur biaya saja yang diperhitungkan, maka hasil yang diperoleh disebut capitalized cost (biaya modal). Metode tersbut mempermudah perbandinga alternative dengan usia pakai yang tak terhingga, dimana asumsi perulangan sulit untuk diterapkan.

Capitalized worth adalah sejumlah uang yang harus dimiliki saat ini. Dengan demikian, diperoleh pembayaran yang besarnya sama selama periode tak terhingga pada tingkat suku bunga i% per periode.

Dari factor bunga majemuk untuk nilai n tak terhingga, didapatkan nilai (P/A,i,n) = 1/I sehingga:

ü  Contoh :

Sebuah perusahaa akan membeli sebuah mesin untuk meninggalkan pendapatan tahunannya. Dua alternative mesin ditawarkan kepada perusahaan:

Mesin	Usia pakai (tahun)	Harga beli (Rp.)	Keuntungan per tahun (Rp.)	Nilai sisa pada akhir usia manfaat (Rp.)
X	8	2.500.000	750.000	1.000.000
Y	9	3.500.000	900.000	1.500.000

Dengan tingkat suku bunga 15% per tahun dan periode analisis tak terhingga, tentukan mesin yang seharusnya dibeli.

Penyelesaian:

CW_X = 750.000(P/A,15%,∞) + 1.000.000(A/F,15%,8)(P/A,15%,∞) –2.500.000(A/P,15%,8)(P/A,15%,∞)

CW_X = 750.000(1/0.15) + 1.000.000(0.07285)(1/0.15) –2.500.000(0.22285)(1/0.15)

CW_X = 1771500

Mesin Y:

CW_Y = 900.000(P/A,15%,∞) + 1.500.000(A/F,15%,8)(P/A,15%,∞) – 3.500.000(A/P,15%,8)(P/A,15%,∞)

CW_Y = 900.000(1/0.15) + 1.500.000(0.05957)(1/15) –3.500.000(0.20957)(1/0.15)

CW_Y = 1.705.733,33

Konsep Annual Worth Analysis

Annual Worth Analysis Metode Annual Worth (AW) 

Annual Worth Analysis Metode Annual Worth (AW) atau disebut juga
Annual Equivalent yaitu metode dimana aliran kas masuk dan kas keluar didistribusikan dalam
sederetan nilai uang tahunan secara merata (sama besar), setiap periode waktu sepanjang
umur investasi, pada suatu tingkat pengembalian minimum yang diinginkan
(MARR).

Istilah Capital Recovery (CR)

CR adalah Nilai merata tahunan yang ekuivalen dengan modal  yang   diinvestasikan.

CR = I(A/P, i, n) – S(A/F, i, n)

CR = (I-S) (A/F, i, n) + I(i)

CR = (I-S) (A/P, i, n) + S(i)

• I : Investasi awal
• S : Nilai sisa di akhir usia pakai
• n : Usia pakai

AW = Revenue –Expences -CR

Annual Worth Analysis dilakukan terhadap:

1. Alternatif tunggal , layak jika AW > 0

2. Beberapa alternatif dgn usia pakai sama

3. Beberapa alternatif dgn usia pakai berbeda

4. Periode analisis tak berhingga

Untuk 2,3, dan 4 : dipilih AW terbesar

Contoh

1. Sebuah mesin memiliki biaya awal sebesar 1 juta rupiah, dengan usia pakai 10 tahun. Nilai sisa

pada akhir usia adalah 200 ribu rupiah. Dengan tingkat suku bunga 10% per tahun, tentukan besar

capital recoverynya.

2. Sebuah perusahaan sedang mempertimbangkan untuk membeli peralatan baru seharga 30 juta

rupiah. Dengan peralatan baru tersebut akan diperoleh penghematan sebesar 1 juta rupiah per 

tahun selama 8 tahun. Pada akhir tahun ke-8  peralatan itu memiliki nilai jual 40 juta rupiah. 

Apabila tingkat suku bunga 12% per tahun,  dengan Annual Worth Analysis, apakah pembelian

peralatan tersebut menguntungkan?

3. Sebuah perusahaan akan membeli sebuah mesin untuk meningkatkan pendapatan tahunannya. Dua alternatif mesin dengan usia pakai masing-masing 8 tahun ditawarkankepada perusahaan:

•  Mesin-x dengan harga beli 2,5 juta rupiah,  keuntungan per tahun 750 ribu rph, nilai sisa padaakhir usia manfaat 1 juta rph.
• Mesin-y dengan harga beli 3,5 juta rph,  keuntungan per tahun 900 ribu rph, nilai sisa pada akhir usia manfaat sebesar 1,5 juta rupiah.

Dengan tingkat suku bunga 15% per tahun, tentukan mesin yang seharusnya dibeli?

Contoh usia pakai berbeda

4. Sebuah perusahaan akan membeli sebuah mesin untuk meningkatkan pendapatan tahunannya. Dua alternatif mesin ditawarkan kepada perusahaan:

• Mesin-x usia pakai 8 tahun dengan harga beli 2,5  juta rupiah, keuntungan per tahun 750 ribu rph, nilai sisa padaakhir usia manfaat 1 juta rph. 
• Mesin-y usia pakai 9 tahun dengan harga beli 3,5  juta rph, keuntungan per tahun 900 ribu rph, nilaisisa pada akhir usia manfaat sebesar 1,5 juta rupiah.

Dengan tingkat suku bunga 15% per tahun, tentukan mesin yang seharusnya dibeli?

Contoh Analisis Tak berhingga. 6. Bandingkan tiga alternatif berikut menggunakan tingkat

suku bunga 10% per tahun, lalu pilih alternatif terbaik:

•  Alternatif-A Investasi awal $1 juta, keuntungan tahunan $150 ribu, usia pakai tak berhingga.
• Alternatif-B Investasi awal $1,5 juta, keuntungan tahunan $250 ribu, usia pakai 14 tahun. 
• Alternatif-C Investasi awal $2,5 juta, keuntungan tahunan $500 ribu, usia pakai 9 tahun.

Alternatif B dan C menggunakan asumsi perulangan dengan konsekuensi ekonomi yang selalu sama.

CASH FLOW

 PERHITUNGAN NILAI NPV BERDASARKAN CASH FLOW DIAGRAM

CONTOH PERHITUNGAN

Berdasarkan hasil penelitian yang digunakan untuk membangun industri pengolahan usaha, diketahui:

Dana investasi : Rp 35,000,000,- (dialokasikan selama 2 tahun)

Tahun persiapan Rp 20,000,000,-

Tahun pertama Rp 15,000,000,-

Kegiatan pabrik dimulai setelah tahun kedua dari pengembangan kontruksi

Jumlah biaya operasi dan pemeliharaan berdasarkan rekapitulasi dari berbagai biaya pada tahun kedua sebesar Rp 5,000,000,- /tahun dan untuk tahun-tahun berikutnya seperti pada tabel 1.

Benefit dari kegiatan industri ini adalah jumlah produksi dari pengolahan hasil-hasil pertanian, Kegiatan produksi dimulai pada tahun kedua dengan jumlah penghasilan Rp 10,000,000,- sedangkan pada tahun-tahun berikutnya seperti pada tabel 1, Berdasarkan data diatas, apakah rencana pembukaan industri yang mengolah hasil pertanian tersebut layak untuk dikembangkan bila dilihat dari segi NPV denga diskon factor sebesar 18%?

JAWAB:

Untuk menghitung nialai NPV proyek tersebut digunakan rumus sebagai berikut:

NPV= _I (1+i)^-n

NPV= 11.115.000

Nilai NPV adalah 11.115.000 dengan nilai NPV ini adalah lebih dari satu, maka gagasan usaha proyek tersebut layak untuk diusahakan

Catatan:

• Perkiraan cash in flow dan cash out flow yang menyangkut proyeksi harus mendapat perhatian.
• Perkiraan beefit harus diperhitungkan dengan menggunakan berbagai variabel (perkembangan proyeksi sejenis dimasa yangakan datang, perubahan teknologi, perubahan konsumen).

Karena dapat catatan untuk memperhatikan cash flow-nya maka dihitung mengunakan cash flow diagram

Perhitungan juga dapat dilihat mengunakan perhitungan dalam tabel berikut:

Tabel 1.  Persiapan Perhitungan NPV

Thn	Investasi *	Biaya Operasi *	Total coast *	Benefit *	Net benefit *	D,F * 18%	Present value *
0	20.000	-	20.000	-	-20.000	1,0000	-20.000
1	15.500	-	15.500	-	-15.500	0,8475	-12.713
2	-	5.000	5.000	10.000	5.000	0,7182	3.591
3	-	6.000	6.000	12.000	6.000	0,6086	3.652
4	-	6.000	6.000	14.000	8.000	0,5158	4.126
5	-	7.000	7.000	17.000	10.000	0,4371	4.371
6	-	7.000	7.000	21.000	14.000	0,3704	5.186
7	-	8.000	8.000	25.000	17.000	0,3139	5.336
8	-	9.000	9.000	30.000	21.000	0,2660	5.586
9	-	10.000	10.000	36.000	26.000	0,2255	5.863
10	-	11.000	11.000	43.000	32.000	0,1911	6.115
NPV							11.115,73

*(dalam Rp,000,-)

Nilai NPV adalah 11.115,73

Nilai NPV > 1, maka gagasan usaha proyek tersebut layak untuk diusahakan.

Maka nilai P bisa dihitung dengan mengunakan rumus pada tabel bunga, sebagai berikut:

P = – 2.000 + (-15.000(P/F.i.n)) + (-5000(P/F.i.n)) + (-6000(P/A.i.n)) (P/F.i.n)

+ (-7000(P/A.i.n)) (P/F.i.n) + (-8000(P/F.i.n)) + (-9000(P/F.i.n))

+ (-10000(P/F.i.n)) + (-11000(P/F.i.n))

Maka dari tabel didapatkan nilai pengeluaranya adalah  sebagai berikut:

P = -58.015.03

Perhitungan NVP  dari cash in flow adalah sebagai berikut:

Dari cash in flow tersebut dapat kita hitung present value proyek tersebut dengan rumus sebagai berikut:

P  = 10.000 (P/F.i.n)) + (12.000 (P/F.i.n)) + (14.000 (P/F.i.n)) + (17.000 (P/F.i.n))

+ (21.000 ( (P/F.i.n)) + ( 25.000(P/F.i.n)) + (30.000 (P/F.i.n))

+ (-36.000 (P/F.i.n)) + (-43.000 (P/F.i.n))

Maka dari tabel diapatkan nilai present value di atas adalah :

P = 69.078.3

Maka NPV      = 69.078.3-58.015.03

= 11.063,27

Dari perhitungan terdapat perbedaan dengan nilai yang dihitung menggunakan rumus bunga. Hal itu disebabkan pada tabel pengeluaran pada tahun ke-3 dan ke-4 tidak dijadikan nilai present terlebih dahulu melainkan langsung diperhitungkan, begitupun pada tahun ke-5 dan ke-6.